Habitación Científica: Números taxicab

martes, 14 de febrero de 2012

Números taxicab

Desde el encuentro en la clínica entre Ramanujan y Hardy, a los números que tienen la propiedad de ser los mas pequeños que se pueden expresar como suma de n cubos de dos maneras diferentes se les llama taxicab y se definen así: «El número taxicab n-ésimo es el numero natural mas pequeño que se puede expresar de n formas distintas como la suma de dos cubos positivos.» Actualmente los números taxicab conocidos son:

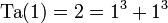
$\operatorname{Ta}(1) = 2 = 1^3 + 1^3$

$\begin{matrix}\operatorname{Ta}(2)&=&1729&=&1^3 + 12^3 \\&&&=&9^3 + 10^3\end{matrix}$

$\begin{matrix}\operatorname{Ta}(3)&=&87539319&=&167^3 + 436^3 \\&&&=&228^3 + 423^3 \\&&&=&255^3 + 414^3\end{matrix}$

$\begin{matrix}\operatorname{Ta}(4)&=&6963472309248&=&2421^3 + 19083^3 \\&&&=&5436^3 + 18948^3 \\&&&=&10200^3 + 18072^3 \\&&&=&13322^3 + 16630^3\end{matrix}$

$\begin{matrix}\operatorname{Ta}(5)&=&48988659276962496&=&38787^3 + 365757^3 \\&&&=&107839^3 + 362753^3 \\&&&=&205292^3 + 342952^3 \\&&&=&221424^3 + 336588^3 \\&&&=&231518^3 + 331954^3\end{matrix}$

$\begin{matrix}\operatorname{Ta}(6)&=&24153319581254312065344&=&582162^3 + 28906206^3 \\&&&=&3064173^3 + 28894803^3 \\&&&=&8519281^3 + 28657487^3 \\&&&=&16218068^3 + 27093208^3 \\&&&=&17492496^3 + 26590452^3 \\&&&=&18289922^3 + 26224366^3\end{matrix}$